Answer : A
Explanation
Hem de tenir present que és quan dos o més condicions són favorables. Això vol dir que S = 1, H = 0 o T = 1
La prova consta de dues parts, amb dos exercicis a cadascuna. La primera part és comuna i la segona té dues opcions (A i B). Resoleu els exercicis de la primera part i, per a la segona part, escolliu UNA de les dues opcions (A o B) i feu els exercicis de l’opció triada.
PRIMERA PART
Exercici 1
[2,5 punts]
[En cada qüestió només es pot triar UNA resposta. Qüestió ben contestada: 0,5 punts; qüestió mal contestada: –0,16 punts; qüestió no contestada: 0 punts.]
Qüestió 1 - Un cargol de pas p = 1,25 mm avança a una velocitat v = 5 mm/s quan es cargola a una femella fixa. Quina és la velocitat angular de gir del cargol?
Explanation
Sabem que una volta són 1,25 mm i que va a 5 mm/s. És fa un factor de conversió a radians
Qüestió 2 - Una empresa comercialitza un model nou d’impressora 3D. El cost unitari de producció és de 500 €. Durant el primer any, l’empresa vol recuperar 250 000 € de la inversió inicial, obtenir un benefici mínim de 50 000 € i pagar les despeses de fabricació de totes les unitats venudes. Si s’ha fixat un preu de venda unitari de 950 €, quin ha de ser el nombre mínim d’unitats venudes?
Explanation
Per calcular el total d'unitats hem de sumar el benefici que volme trobar (250000+50000) i dividirlo entre el benefici per unitat (950-500)
Qüestió 3 - Una barra massissa de secció circular de 5 mm de radi pot aguantar una força de tracció de fins a 8,1 kN sense trencar-se. Quina és la resistència a la ruptura del material de la barra?
Explanation
Apliquem la formula de la pressió = F/A
Qüestió 4 - Un motor asíncron de corrent altern de p = 4 parells de pols té un lliscament relatiu s = 0,07. Si està connectat a la xarxa de tensió U = 230 V i freqüència f = 50 Hz, a quina velocitat n gira?
Explanation
Primer hem de saber la velocitat de sincronisme i el seguent pas, dintre del lliscamnet relatiu aïllar la "n" que és la velocitat de gir
Qüestió 5 - Un cilindre hidràulic d’una sola tija ha de poder efectuar una força de 25 kN en la cursa d’avanç. Si el diàmetre del cilindre és de 40 mm i el de la tija és de 25 mm, quina pressió ha de proporcionar el grup hidràulic?
Explanation
La formula de la pressió és F/A
Exercici 2
[2,5 punts]
Un sistema de reg inteŀligent utilitza tres sensors per a determinar si cal regar un parc d’una ciutat al final del dia. Els sensors mesuren la radiació solar (S), la humitat del terra (H) i la temperatura (T). Les condicions ambientals favorables al reg són: una radiació solar per sobre d’un llindar Slim, una humitat del terra per sota de Hlim i una temperatura per sobre de Tlim. El sistema determina que cal regar si almenys dues de les tres condicions ambientals són favorables al reg. Responeu a les qüestions que hi ha a continuació utilitzant les variables d’estat següents:
Explanation
Hem de tenir present que és quan dos o més condicions són favorables. Això vol dir que S = 1, H = 0 o T = 1
b) - Determineu la funció lògica entre aquestes variables i, si escau, simplifiqueu-la. [1 punt]
a) r = s·h(negada) + s·t(negada) + ht
b) r = s·h(negada) + s·t + h(negada)·t
Explanation
Quan posem a la tabla en ordre el que ens ha donat la taula, observem el resultat on: x2 és la primera entrada (S), x0 la segona entrada (H) i x1 la tercera entrada (T)
Explanation
Són tres sumes amb dos elements multiplicats entre sí. Gràcies a Karnaugh ens donem compte que la H sempre negada i les altres dues multiplicant-se.
SEGONA PART
OPCIÓ A
Exercici 3
[2,5 punts en total]
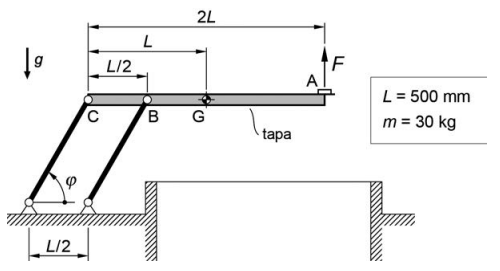
La tapa de la figura té una massa m = 30 kg i el centre de masses en el punt G. S’obre estirant-la per la nansa A amb una força F perpendicular a la tapa, i s’uneix a terra per mitjà de dues barres idèntiques que tenen un extrem articulat a la tapa i l’altre extrem articulat a terra. La massa de les barres es considera negligible. L’angle de les barres varia entre 10° ≤ φ ≤ 120°
a) Dibuixeu el diagrama de cos lliure de la tapa per a un angle φ qualsevol. [0,5 punts]
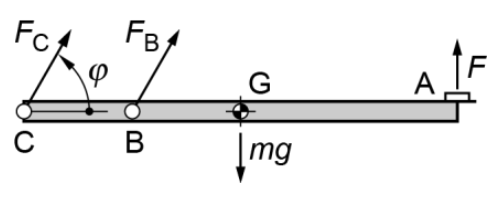
Considerant que la tapa està en repòs, determineu:
b)El valor de la força F aplicada a la nansa quan φ = 60°. [1 punts]
Tenim el plantegament del problema en dos eixos (x,y):
c)El valor de les forces FB i FC que fan les barres sobre la tapa quan φ = 60°. [0,5 punts]
Per calcular les forcies en un fulcre, el que s'ha de fer es agafar una com un punt fixe i obtindre l'altre. Després substituir.
O bé:
d)L’angle φ per al qual la força que fa la barra en el punt C en valor absolut |FC| és mínima, i el valor d’aquesta força. [0,5 punts]
Per trobar un angle on la força sigui minima, haurem de trobar el factor que l'altera (l'angle), aquest es troba en denominador dintre de la funció sinφ. Per fer aixó trobarem l'angle per fer màxim la funció. Les regles trigonométriques ens diu que és quan el sinus val 90° o 270° (Nosaltres ens fixem en el primer quadrant).
Exercici 4
[2,5 punts en total]
Un escalfador elèctric d’aigua s’alimenta amb una tensió U = 230 V i consumeix una potència elèctrica Pelèctr = 1,5 kW. L’escalfador tarda 2 h i 5 min a escalfar un volum V= 50 L d’aigua des de T1 = 15 °C fins a T2 = 65 °C per mitjà d’una resistència elèctrica. La calor específica de l’aigua és ce = 4,18 kJ/(kg °C) i el cost de l’energia elèctrica és c = 0,125 /(kW h).
determineu:
a)L’energia E necessària per a escalfar el volum V d’aigua des de T1 fins a T2. [0,5 punts]
b)L’energia elèctrica Eelèctr, en kW h, consumida per a escalfar el volum V d’aigua des de T1 fins a T2 , i el cost celèctr de l’energia elèctrica necessària per a dur a terme aquest procés. [0,5 punts]
c)El rendiment η de l’escalfador elèctric d’aigua. [0,5 punts]
d)La resistivitat ρ del material de la resistència, si aquesta està formada per un fil conductor de diàmetre d = 0,25 mm i longitud L = 1 500 mm. [1 punt]
OPCIÓ B
Exercici 3
[2,5 punts en total]
Una escala mecànica transporta passatgers que pugen una altura Δh = 6 m en un temps tp = 45 s. La massa mitjana d’un passatger s’estima en mp = 70,8 kg. L’escala transporta de mitjana np = 20 passatgers de manera simultània i funciona durant tt = 10 h al dia.
Quan l’escala treballa en buit (sense passatgers) consumeix una potència elèctrica Pbuit = 3,2 kW. El grup motor (motor, reductor i transmissió) que acciona l’escala té un rendiment electromecànic η = 0,58. Determineu:
a)La potència mecànica mitjana Pp addicional que cal per a pujar de manera simultània np = 20 passatgers. [1 punt]
b)El nombre total nt de passatgers que l’escala transporta en un dia. [0,5 punts]
c)L’energia elèctrica total Et que consumeix l’escala en un dia, considerant el consum elèctric en buit i el consum associat a pujar els passatgers. [1 punt]
Exercici 4
[2,5 punts en total]
Un vehicle consumeix una mitjana de 6,3 L cada 100 km quan circula a una velocitat v = 120 km/h. El dipòsit de combustible del vehicle té una capacitat V= 60 L. El vehicle té la tracció a l’eix davanter i, per a la velocitat v anterior, les rodes giren a una velocitat angular nrodes = 1 004 min–1 (considerant que el vehicle avança en línia recta). Entre el motor tèrmic i les rodes hi ha una transmissió mecànica de rendiment ηtrans = 0,92, i el rendiment tèrmic del motor és ηmot = 0,30. El combustible utilitzat té una densitat ρ = 0,75 kg/L i un poder calorífic pc = 43,5 MJ/kg. Si el vehicle circula a una velocitat v = 120 km/h, determineu:
a)La distància estimada d que pot recórrer el vehicle si el dipòsit conté combustible fins al 80 % de la seva capacitat. [0,5 punts]
b) La potència tèrmica mitjana consumida Ptèrm. [0,5 punts]
c) La potència mecànica que arriba a les rodes Prodes i el parell total Γrodes. [1 punt]
Dividim el problema en dues part
La potència mecànica a les rodes
Existeixen dos rendiments que arriben a les rodes: El rendiment tèrmic que passa del que genera aquest calor (combustible) al motor (on es perd potència). I aquesta potència tèrmica que impulsa el motor arriba també a les rodes (Potència de les rodes) però es perd potència per fricció ... Per tant apliquem un altre rendiment (Rendiment de les rodes)
d)La potència total que es dissipa en el motor i en la transmissió Pdiss. [0,5 punts]
Sabem que quan hi ha un congunt de rendiments es poden sumar totes les potencies disipades o bé calcularles. També, si aquests rendiments estan seguits (com es el nostre cas) es poden restal la incial menys la final. En cas contrari s'haurien de tornar a calcular totes